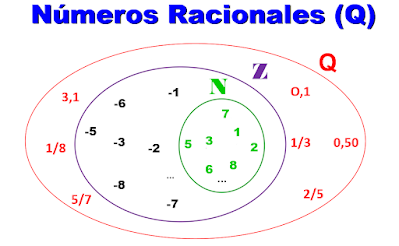
Los números Racionales son todos aquellos números que se pueden representar como fracción.
LOS NÚMEROS NATURALES.
Son los números básicos que el hombre hace para contar y ordenar los objetos.
Se representa por la letra "N".
N = { 0 ; 1 ; 2 ; 3 ; 4 ; 5 ... ∞ }
LOS NÚMEROS ENTEROS.
Son los números positivos y negativos. Incluye a "N".
Se representa por la letra "Z".
Z = { ∞ ; ... ; -3 ; -2 ; -1 ; 0 ; 1 ; 2 ; 3 ; ... ; ∞ }
LOS NÚMEROS RACIONALES.
Son los números positivos y negativos. Incluye a los números decimales y a las fracciones. Incluye a "N" y "Z".
Se representa por la letra "Q".
Q = { ∞ ; ... ; -3 ; -2 ; -1 ; -0,5 ; 0 ; 1/2 ; 1 ; 1,5 ; 2 ; 3 ; ... ; ∞ }
Todos los elementos del conjunto de los números racionales pueden ser expresados como una fracción de la forma a/b, donde a, b ∈ Ζ y b ≠ 0.
Por ejemplo:
El número fraccionario -3/8 es un número racional, ya que -3 y 8 ∈ Ζ y 8 ≠ 0. También, -3/8 puede ser expresado como el número decimal -0,375.
Observa la inclusión de los conjuntos:
Un número racional se puede representar por infinitas fracciones con similar valor numérico, es decir, por fracciones que sean equivalentes.
Por ejemplo, 1/2 puede ser expresado como 2/4 ; 4/8 ; 5/10 ; etc.
Es importante mencionar que los números enteros también pueden ser expresados como fracción, debido a que todo número entero tiene 1 como denominador; por tanto, son parte de los números racionales.
REPRESENTACIÓN DE LOS NÚMEROS RACIONALES EN LA RECTA NUMÉRICA.
ORDEN DE LOS NÚMEROS RACIONALES
El conjunto de los números racionales es ordenado, pues si se toman dos números racionales cualesquiera, se puede establecer entre ellos una relación de orden; es decir, pueden ser comparados y se puede determinar cuál es el mayor, el menor o si son iguales.
RESUELVE:
¿Cuál es Natural, entero o racional?
-0,7 ; 8 ; 1/3 ; 2 ; 6,25 ; -3
SOLUCIÓN: